Алексей Дмитриевич Кондорский, Отделение оптики ФИАН
Введение
Целью оптического управления является подбор такого лазерного поля, чтобы при взаимодействии с ним атом или молекула перешла в требуемое квантовое состояние, либо заданным образом изменилась выработка продуктов в реакции, ориентация молекулы и пр. В настоящее время главной целью является разработка методов управления такими сложными объектами, как многоатомные молекулы, белки, наноразмерные структуры, синтез новых соединений и разработка лекарственных средств и т.д.
Развитие методов лазерного управления началось сразу после изобретения лазера. Если первыми задачами поставленными еще в 1960х годах были задачи селективного заселения отдельных состояний молекул, то в настоящее время ставятся задачи селективного разрыва и создания молекулярных связей в многоатомных молекулах. В последнем случае сложность состоит в том, что разные степени свободы в многоатомной молекуле обычно сильно связаны друг с другом. Поэтому даже быстрое возбуждение отдельной химической связи коротким лазерным импульсом часто приводит не менее быстрому перераспределению возбуждения между другими связями. Это неизбежно стимулирует конкурирующие побочные процессы, которые сводят на нет эффективность оптического управления.
В настоящее время эта проблема решается путем создания таких управляющих лазерных полей, которые приводят к когерентному возбуждению сразу нескольких связей в многоатомной молекуле. Это позволяет использовать эффект интерференционного усиления для достижения нужного результата.
Основная идея когерентного оптического управления молекулярными процессами
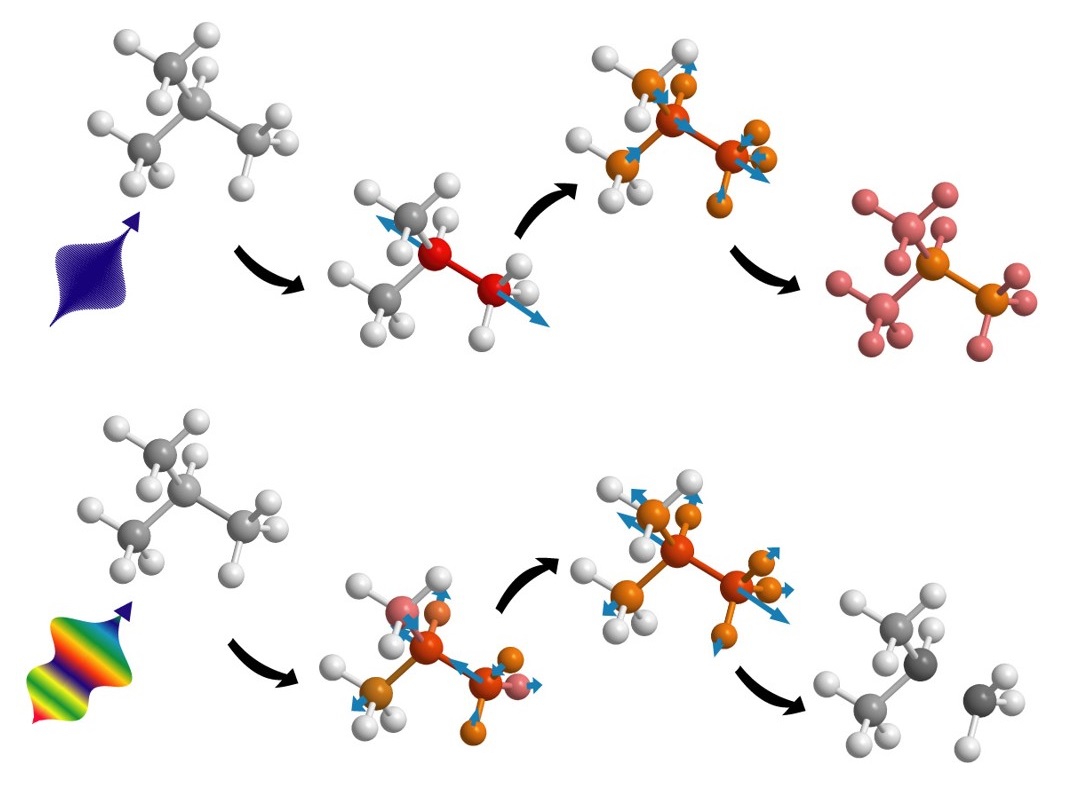Данный рисунок поясняет эту идею. При «классическом» селективном по модам фотохимическом процессе лазерный импульс с узким спектром селективно возбуждает нужную химическую связь. Если эта мода молекулы слабо связана с другими, то поле раскачивает атомы и разрывает связь между ними. К сожалению, так происходит лишь в простейших молекулярных системах, например в тех у которых массы связанных ядер значительно отличаются. В большинстве же молекул возбуждение быстро передается соседним связям и энергия теряется. Фактически лазер всего лишь нагревает молекулу. При этом стимулируется множество побочных процессов и теряется желаемая селективность.
Однако если при подборе управляющего лазерного импульса учесть взаимодействие между связью, которую нужно разорвать, и соседними, то можно подобрать более сложный, обычно широкополосный, лазерный импульс, который заданным образом возбудит всю группу связей. Такое возбуждение вызовет интерференцию между движениями соседних ядер и в результате взаимного усиления произойдет разрыв нужной связи. При более корректном описании, конечно, следует говорить об управлении интерференционными эффектами многопараметрической волновой функции всей молекулы для усиления нужного и подавления конкурирующих процессов. Таким образом, оптическое управление именно квантовыми интерференционными эффектами является наиболее эффективным способом управления молекулярными процессами.
Хотя задача и является достаточно сложной, она успешно решается как теоретически, так и экспериментально. В последнее время значительный прогресс в этой области связан с развитием вычислительной техники и её широкого внедрения в эксперимент, разработкой эффективных оптимизационных и генетических самообучающихся алгоритмов, а так же началом промышленного выпуска приборов для генерации широкополосных фемтосекундных лазерных импульсов с программируемой амплитудной и частотной зависимостью от времени.
Фазовое управление Брумера и Шапиро
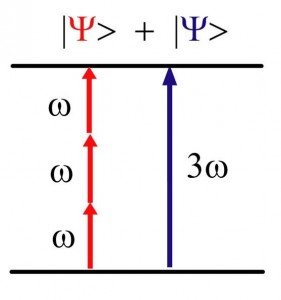В качестве простого примера квантового оптического управления рассмотрим селективное заселение уровня при помощи фазового управления по схеме Брумера-Шапиро [Brumer, M. Shapiro, Chem. Phys. Lett. 126, 541 (1986); Shapiro, et. al. Chem. Phys. Lett. 149, 451 (1988)]. Этот подход напрямую использует эффект интерференции волновой функции, возникающий если переход c начального уровня на требуемый может происходить несколькими путями. Особенностью метода является возможность селективного заселения отдельных энергетически вырожденных уровней или узких полосок континуумов, соответствующих разным продуктам диссоциации. В простейшем случае для управления используются два монохроматических лазерных поля одно с частотой равной резонансной частоте перехода между начальным и конечным уровнем и второе с частотой в три раза меньшей. При изменении разницы фаз между двумя полями происходит изменение фаз между амплитудами населенностей перешедших из начального состояния во конечные по одному и другому пути. При этом возникает интерференция сложения и вычитания этих амплитуд и конечная наблюдаемая населенность разных состояний конечного вырожденного уровня колеблется.
Преимущество этой схемы состоит в том, что, во-первых, можно добиться селективного заселения отдельных вырожденных состояний. В случае если это состояния непрерывного спектра, это будет соответствовать выбору того или иного канала диссоциации. И, второе, что процесс происходит при меньших интенсивностях управляющих полей, чем он происходил бы в отсутствии эффекта интерференции амплитуд конечных состояний. Конечно, поскольку эффективность управления зависит от спектроскопических характеристик переходов, то схема фазового управления хорошо работает не для всяких систем. Схема Брумера-Шапиро была экспериментально реализована для атомов и малых молекул.
Стимулированный быстрый адиабатический переход (STIRAP)
Другой пример схемы для селективного заселения уровня является стимулированный быстрый адиабатический переход [Gubatz, et. al. Chem. Phys. Lett. 149, 463 (1988);Bergmann, H. Theuer, B. W. Shore, Rev. Mod. Phys. 70, 1003 (1998)].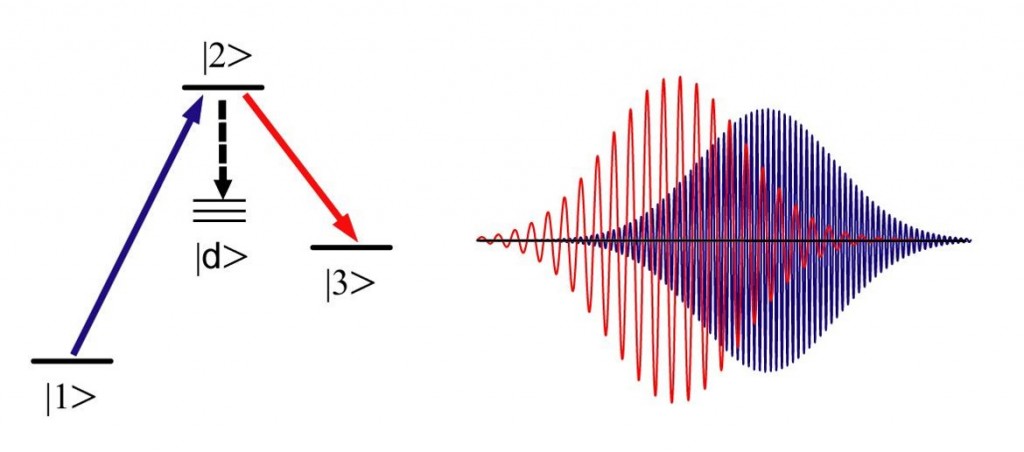 
В первоначальной форме схема предназначена для полного переноса населенности из одного состояния в другое через промежуточный уровень. Для этого используется два импульса со специально подобранной задержкой между ними. Первый импульс связывает начальное состояние 1 с промежуточным состоянием 2. Второй связывает промежуточное состояние 2 с конечным состоянием 3. Оба импульса должны быть сильными, так чтобы в длительность всего процесса была много больше периода Раби для обоих переходов. Если это условие адиабатичности выполнено, то можно достигнуть полного переноса населенности из состояния 1 в состояние 3. Вопреки интуиции, для этого необходимо чтобы, во-первых оба лазерных импульса находились не в точном резонансе с частотами соответствующих переходов, и во-вторых второй импульс должен начаться ранее, чем первый. Преимущество этой схемы состоит в том, что в течение всего процесса населенность промежуточного состояния практически равна нулю. Таким образом, даже при наличии сильных переходов из промежуточного состояния на другие уровни потерь за счет этого не происходит.
Метод накачки – сброса Таннора, Козлова и Райса
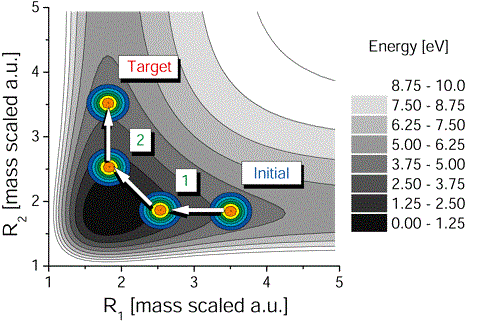
В качестве последнего примера управления при помощи изменения малого числа параметров рассмотрим управление химической реакцией при помощи закачки-сброса [Tannor, S. Rice, J. Chem. Phys. 83, 5013 (1985); Tannor, R. Kosloff, S. Rice, J. Chem. Phys. 85, 5805 (1986)].
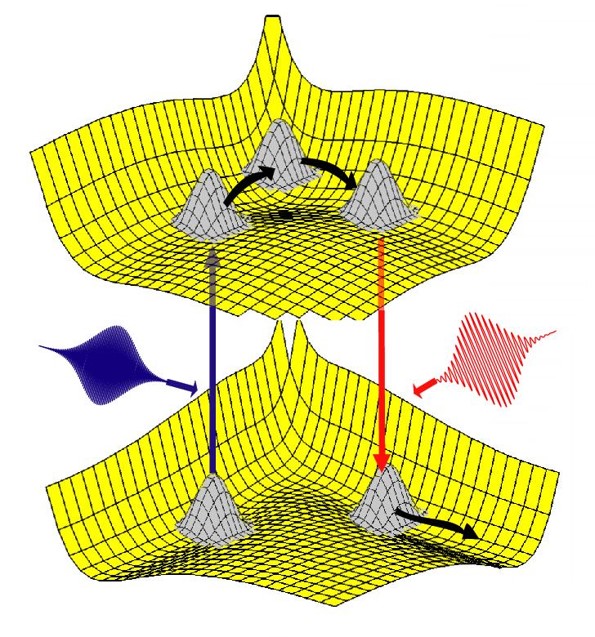Как известно, обычно, динамика молекулярной системы описывается в рамках приближения Бора-Оппенгеймера. Фактически предполагается, что ядра атомов движутся в неких усредненных полях, которые создаются быстро движущиеся электроны. Волновая функция ядер удовлетворяет системе связанных уравнений Шредингера число уравнений, в которых определяется числом описываемых электронных состояний. В данном примере таких состояний два. Размерность координаты при этом равна числу степеней свободы в системы, т.е. растет пропорционально числу образующих ее атомов. В простом случае поведение волнового пакета, описываемое этими связанными уравнениям можно представить себе как его движение по поверхностям потенциальных энергий, которые соответствуют разным электронным состояниям.
В данной схеме волновая функция ядер является суперпозицией колебательных состояний потенциальной ямы, соответствующей начальной устойчивой конфигурации молекулы. Первый лазерный импульс переносит этот волновой пакет в другое электронное состояние. Поскольку поверхность потенциальной энергии здесь не имеет минимума, то он начинает распространяться вдоль некоторой траектории. Это соответствует движению ядер, в новом изменившемся поле, создаваемом электронами. Через некоторое время волновой пакет может достигнуть желаемой конфигурации ядер, которая соответствует устойчивой конфигурации того соединения, которое мы хотели бы получить. В этот момент при помощи второго лазерного импульса молекула переводится в основное электронное состояние. В результате мы получаем либо молекулу в требуемой устойчивой конфигурации, если основное электронное состояние имеет локальный минимум, либо нужные нам продукты распада, если поверхность потенциальной энергии не имеет минимума.
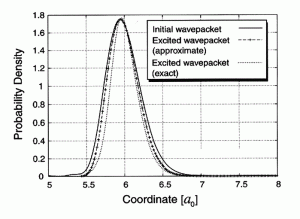Некоторое время назад было показано, что при помощи одного короткого лазерного импульса с квадратичной зависимостью частоты от времени или двух импульсов, одного положительным «чирпом» и другого отрицательным можно крайне эффективно перенести волновой пакет из одного электронного состояния в другое, причем практически без потери его формы скорости и фазы [S.Zou, A. Kondorskiy, G. Mil’nikov, H.Nakamura, J. Chem. Phys. 122, 084112 (2005)]. Преимуществом такого подхода является на порядок меньшие интенсивности управляющих лазерных полей, чем при использовании более простых импульсов. Опять же это достигается за счет положительной интерференции между частями волновой функции возбужденных в начале и в конце взаимодействия с импульсом. На рисунке представлен расчет для случая переноса волнового пакета, являющегося суперпозицией множества колебательных состояний основного электронного терма в первое возбужденное состояние. Как видно, форма волнового пакета при переносе не слишком пострадала. Это в частности удобно для реализации схем подобных схеме накачки-сброса и других.
Получение фемтосекундных лазерных импульсов с программируемой амплитудной и частотной зависимостью от времени
Перечисленные схемы реализуют идею использования эффектов интерференции для управления квантовыми процессами в молекулах в простых случаях. К сожалению, эти методы оказываются применимы не всегда. Для управления квантовыми процессами в молекулах большим числом атомов и сильной связью между разными степенями свободы необходимо использовать лазерное поле с более сложной амплитудной, частотной и фазовой зависимостью. Для генерации таких широкополосных фемтосекундных лазерных импульсов с программируемой зависимостью параметров от времени используются жидкокристаллические оптические модуляторы.
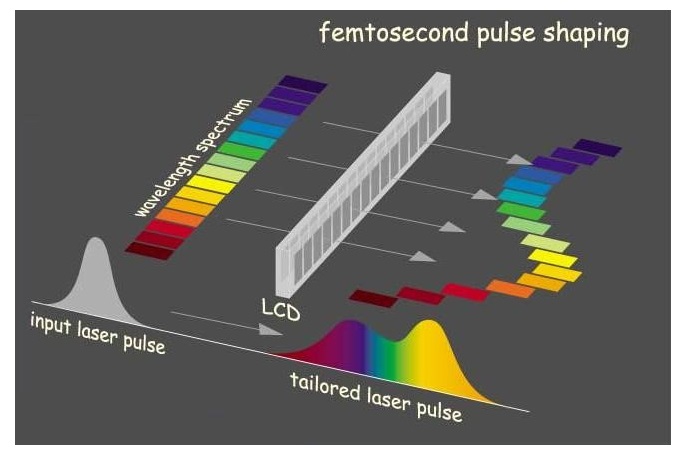Вкратце принцип действия таких приборов можно понять из рисунка. Вначале фемтосекундный лазерный импульс, обладающий достаточно широким спектром разлагается на компоненты с разными длинами волн на дифракционной решетке. Разделенные компоненты собирают на жидкокристаллической матрице, так что разные длины волн падают на разные ячейки. При подаче напряжения на разные ячейки их коэффициенты преломления меняются и соответственно меняются оптические задержки для компонент с разными длинами волн. Поставив за одной матрицей другую, у которой ячейки при подаче напряжения меняют пропускную способность или поляризацию прошедшего излучения можно в широких пределах менять не только фазу, но и амплитуду и поляризацию спектральных компонент и соответственно. Конечный лазерный импульс получается путем сведения всех компонент воедино помощи еще одной дифракционной решетки. В соответствие со свойствами преобразования Фурье зависимости интенсивности, фазы и поляризации конечного импульса от времени определяются напряжениями, поданными на ячейки жидкокристаллической матрицы.
Обычно используются матрицы с числом ячеек 128, каждая из которых управляется 12 битной последовательностью. Таким образом, число возможных видов импульсов, которые можно генерировать таким прибором оказывается порядка 10 в 400 степени. Описанные приборы выпускаются промышленно для спектрального диапазона от 430 нм до 1,6 мкм.
Основные вопросы и ответы
Коль скоро существует возможность создавать лазерные поля с программируемыми зависимостями параметров от времени возникает вопрос, возможно ли управлять произвольной сложной молекулярной системой и если можно, то как это сделать? Ведь нельзя же каждый раз перебирать все 10 в 400 типов импульсов.
К сожалению, невозможно а приори сказать до какой степени возможно управлять той или иной квантовой системой. Доказана лишь одна теорема, определяющая достаточное, но не необходимое условие существования управляющего поля. Доказано, что если система локализована в пространстве, и, следовательно в отсутствие внешнего поля обладает только дискретными уровнями которые связаны друг с другом оптическими переходами того или иного типа, то существует внешнее поле, которое позволяет преобразовать любую заданную начальную волновую функцию в любую заданную конечную волновую функцию. Однако это означает, что можно управлять только такими системами.
Впрочем, интерес к дальнейшему поиску доказательств существования управляющих полей почти прекратился в связи с тем, что уже в конце 80х годов теоретиками были предложены крайне эффективные методы расчета управляющих лазерных полей для самых разных квантовых систем. В результате объединения этих методов была разработана теория оптимального оптического управления, о которой я расскажу подробно чуть позже. Наряду с теорией оптимального управления в начале 90х годов было предложено использовать для поиска управляющих полей так называемые генетические алгоритмы. Вначале эффективность такого подхода была продемонстрирована теоретически. Однако в начале века с распространением в лабораториях жидкокристаллических оптических модуляторов начался целый бум, связанный с чисто экспериментальной реализацией лазерного управления сложными молекулами при помощи генетических кодов.
Управление при помощи генетических самообучающихся алгоритмов
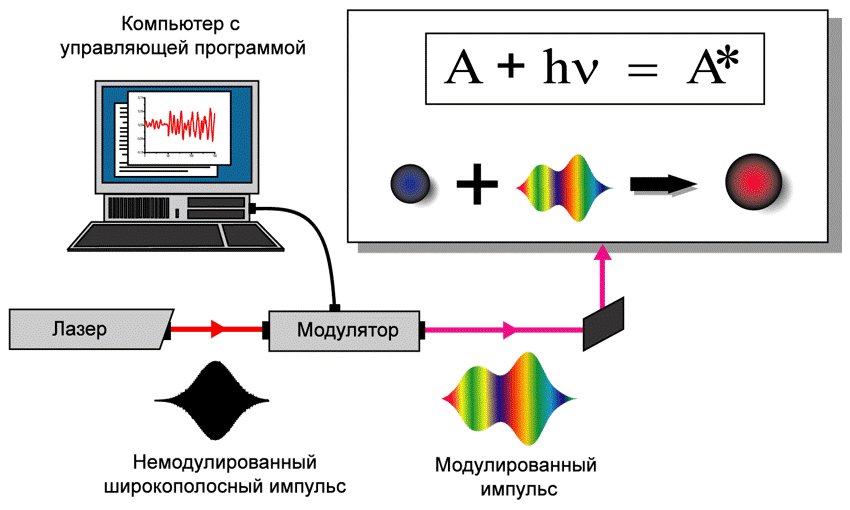
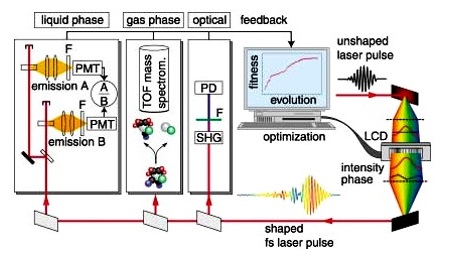Вот типичная схема такого эксперимента [Judson, H. Rabitz, Phys. Rev. Lett. 68, 1500 (1992); Обзор: T. Brixner, G. Gerber, Chem. Phys. Chem. 4, 418 (2003)]. Компьютер формирует лазерные импульсы с помощью описанного ранее устройства. Значение измеряемой в эксперименте физической величины вводится обратно в компьютер. Генетический самообучающийся алгоритм анализирует отклик физической величины на изменения параметров генерируемого лазерного излучения и подбирает параметры лазерного излучения так чтобы максимизировать или минимизировать его.
При помощи такого рода экспериментов за последние несколько лет получены весьма впечатляющие результаты в области управления самыми разными молекулярными системами, как в газовой фазе, так и в жидкости. В последнее время такая схема применяется и для несколько неожиданных целей, а именно для генерации аттосекундных импульсов с заданными параметрами. Такие импульсы возникают в результате нелинейного взаимодействия сильных фемтосекундных импульсов со средой. Например, часто используется эффект надпороговой ионизации атомов. Понятно, что для того, чтобы получить аттосекундный импульс определенной формы необходимо подобрать подходящий начальный фемтосекундный импульс. За последние два года использование генетических самообучающихся алгоритмов привело к значительному прогрессу в этой области.
Принципы работы генетических алгоритмов
- Генетический код – последовательность битов, т.е. вариант решения задачи.
- Особь – текущее значение конкретного генетического кода
- Воспроизводство – операция, при которой две хромосомы обмениваются своими частями.
- Мутация – случайное изменение одного или нескольких бит в хромосоме.
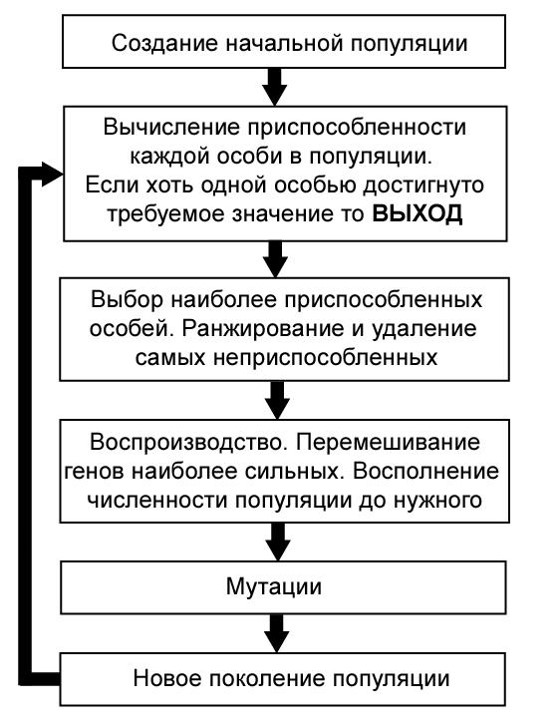Кратко рассмотрим принцип работы генетического самообучающегося алгоритма в его простейшем виде. Из самого названия ясно, что метод является математической метафорой биологической эволюции, приводящей к совершенствованию генетического кода разных животных. В нашем случае генетическим кодом является последовательность бит, управляющая жидкокристаллическим оптическим модулятором. Разные особи популяции несут разный генетический код и представляют собой разные варианты решения задачи управления.
На первом шаге алгоритма мы создаем начальную популяцию. Например генерируем случайным образом множество битовых последовательностей. На втором, для каждой битовой последовательности вычисляется или измеряется приспособленность. В нашем случае это величина физического отклика управляемой системы на лазерные импульсы соответствующие разным генетическим кодам. На третьем шаге все особи, т.е. битовые последовательности ранжируют по уменьшению их приспособленности. Гены наиболее приспособленных особей перемешиваются. Численно это означает, например, что из каждой пары битовых последовательностей формируют две новых последовательности. Для этого комбинируются одни куски из одной последовательности другие из другой. На последнем шаге, некоторые биты в разных последовательностях случайным образом перекидываются, что является метафорой процесса мутации. Мутации являются необходимым элементом эволюции, не позволяющем группе наиболее приспособленных генетических последовательностей перестать совершенствоваться далее.
Таким образом, формируется новое поколение популяции – уже более эффективных вариантов решения задачи. Для этого поколения шаги со второго по пятый проходят снова и снова. Процесс можно прервать, когда в популяции найдутся такие битовые последовательности, которые решают поставленную задачу с заданной эффективностью. Существует большое число реализаций генетических самообучающихся алгоритмов. О них написаны книги.
Теоретическая формулировка задачи в теории оптимального управления
Другим подходом к поиску управляющих лазерных полей, как уже упоминалось, является теория оптимального управления. Теория позволяет рассчитать поле для управления непосредственно волновой функцией квантовой системы. Это позволяет управлять не только наблюдаемыми величинами, но и внутренней квантовой динамикой системы, а так же выяснить физический механизм процесса.
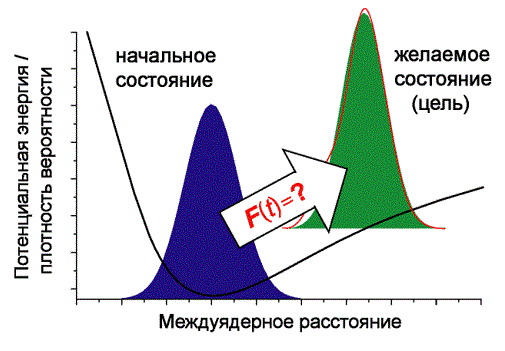Рассмотрим формулировку задачи решаемой теорией на простейшем примере управления движением ядер в двухатомной молекуле иона водорода. Теоретически, процессы, происходящие в этой системе, описываются уравнением Шредингера для волнового пакета, движущегося вдоль потенциальной кривой. Внешнее лазерное поле воздействует на волновой пакет, вызывая его ускорение, смещение и деформацию. Задача управления формулируется следующим образом: задается начальная волновая функция и волновая функция описывающая то состояние системы, которое мы хотим получить (target). Это может быть как некое собственное состояние системы, так и какая-то искусственно заданная функция. Задается интервал времени Т, определяющий длительность физического процесса. Требуется найти такое поле лазера F(t), чтобы волновая функция, удовлетворяющая временному уравнению Шредингера с начальной волновой функцией в конечный момент Т была как можно ближе к волновой функции цели. Фраза «как можно ближе» здесь означает, что величина модуля проекции конечной функции на функцию цели максимальна.
Перед тем как обсуждать методы решения задачи управления, немного забежим вперед и покажем на простых примерах, что поставленная задача может быть решена с высокой эффективностью. В данном примере начальная волновая функция, это функция основного состояния молекулы. В качестве цели взята та же функция, но смещенная на одну атомную единицу. Этот волновой пакет уже представляет собой суперпозицию нескольких возбужденных состояний молекулы. Красным показан волновой пакет, в который перейдет начальная волновая функция под воздействием специально рассчитанного управляющего поля. При этом эффективность процесса составляет 96%. Этот пример показывает, что задача управления может быть успешно решена.
Пример управляющего поля
Во втором примере моделируется реакция обмена c образованием молекулы тяжелой воды. Начальный волновой пакет описывает систему OH на которую налетает атом дейтерия. Волновой пакет цели описывает состояние, когда атом водорода удаляется от молекулы OD. Под воздействием поля эффективность протекания реакции обмена близка к единице, хотя в его отсутствие она составляет несколько процентов [A.Kondorskiy, H. Nakamura, Theor. Comp. Chem. Chem. 4, 75 (2005)].
Теория оптимального управления
Кратко обсудим, как вычисляется управляющее поле в теории оптимального управления. Используется вариационный метод. Суть его в следующем: взаимная проекция конечной волновой функции и функции цели рассматривают как функционал от внешнего поля. Проварьировав его с ограничением, что волновая функция удовлетворяет уравнению Шредингера получают систему уравнений, которая состоит из двух уравнений Шредингера с разными начальными волновыми функциями и формулы внешнего поля [Kosloff, et al, Chem. Phys. 139, 201 (1989); Zhu, J. Botina, H. Rabitz, J. Chem. Phys. 108, 1953 (1998)].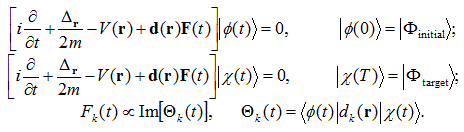
Эту систему можно решать только численно итерационно. При этом, на каждом шаге нужно рассчитать динамику двух волновых пакетов и найти корреляционную функцию между ними.
Управляющие лазерные поля для процессов, которое были приведены выше в качестве примеров, были вычислены именно таким способом. При этом уравнения Шредингера решались точно. К сожалению, подобные квантовомеханические расчеты возможны не более чем для трех- и четырехатомных систем, поскольку необходимые вычислительные мощности при таких расчетах растут экспоненциально с увеличением числа степеней свободы в системе. Эта проблема сильно затормозила дальнейшее развитие теории лазерного управления.
Квазиклассическая теория оптимального управления
- Основывается на использовании квазиклассических методов расчета волновых функций путем интегрирования по классическим траекториям.
- Позволяет теоретически рассчитать поле для управления системами со многими степенями свободы
- Позволяет управлять квантовыми эффектами.
Совсем недавно она была решена путем квазиклассической формулировки теории оптимального управления [Обзор A.Kondorskiy, S.Nanbu, Y.Teranishi, H.Nakamura, J. Phys. Chem. A 114, 6171 (2010)]. Известно, что для описания эволюции волновой функции системы использовался квазиклассический метод основаны на интеграле по траекториям Фейнмана. Идея состоит в представлении волновой функции в виде суммы вкладов множества классических траекторий. Показано, что таким образом можно надежно описать динамику систем с большим числом степеней свободы.
Квазиклассическая теория оптимального управления позволяет эффективно использовать преимущества метода интеграла по траекториям для расчета управляющего лазерного поля. При этом важно отметить, что теория позволяет управлять именно квантовыми эффектами. После тщательной проверки работоспособности теории путем сравнения с результатами точных квантовых расчетов для систем с одной и двумя степенями свободы была решены задачи управления системами с четырьмя и шестью степенями свободы.
Лазерное управление системой с 6 степенями свободы
В качестве примера эффективности теории рассмотрим задачу лазерного управления изомеризацией свободной трехатомной молекулы. Молекула HCN имеет две устойчивые линейные конфигурации представленные на рисунке. Левая конфигурация энергетически более выгода чем правая. Наша цель перевести молекулу из левой конфигурации в правую с максимальной вероятностью.
Подобная задача часто возникает, например, при производстве лекарств. Дело в том, что некоторые соединения обладают двумя конфигурациями. Причем если молекула находится в одной из них, она обладает лечебным действием, а в другом может наоборот вызвать отравление организма (например, левомецитин и правомецитин). При производстве лекарств, обычно обе конфигурации такой молекулы образуются с примерно одинаковыми вероятностями и полученную смесь приходится тщательно фильтровать, чтобы удалить нежелательную компоненту. При этом часто такая фильтрация или очень сложна или вообще не возможна обычными средствами. Использование же лазера является перспективным методом для изменения отношения образующихся конфигураций молекул.
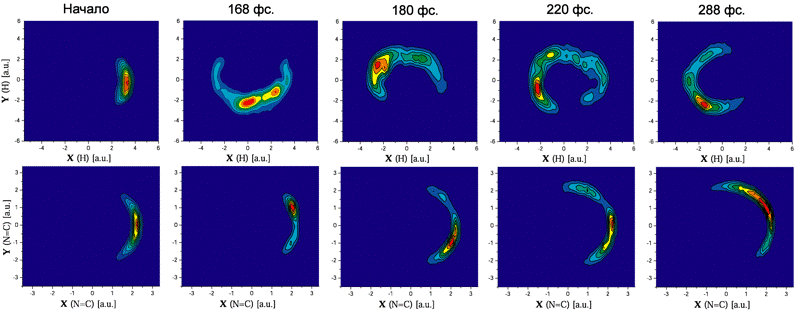
В настоящей задаче молекулы (находящиеся в левом состоянии) предварительно ориентируются слабым лазерным полем. Такие методы известны. Поскольку в процессе изомеризации молекула может вращаться относительно лазера зафиксированного в лабораторной системе координат, то данная система имеет шесть степеней свободы. А именно три координаты вектора от центра масс системы до атома водорода и три координаты вектора проведенного от атома азота к атому углерода.
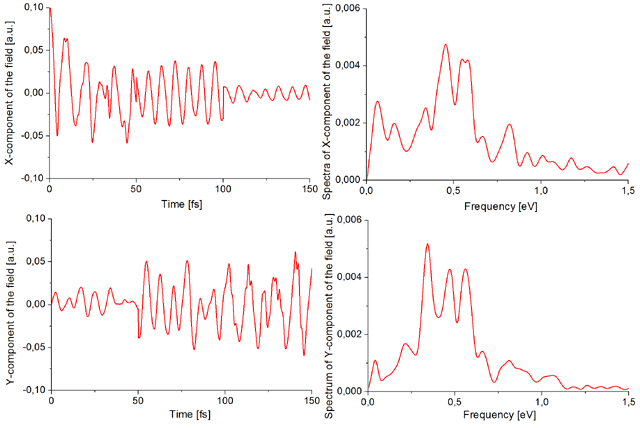
На этом слайде показана динамика управляемого процесса изомеризации. Верхние рисунки показывают плотность вероятности как функцию координат атома водорода в разные моменты времени. Под ними – тоже самое для системы азот и углерод. В низу нарисовано управляющее лазерное поле и его спектр. В результате управления удалось достичь вероятности изомеризации 74%. Управляющее поле имеет две компоненты, что связано с аксиальной симметрией начального состояния системы. Т.е. управление осуществляется эллиптически поляризованным полем. Этот пример показывает, как квазиклассическая теория позволяет управлять всеми шестью степенями свободы системы.